지난 포스팅에 이어 컴퓨터가 사칙연산을 하는 법을 찾아보았다.
예상했던 대로 컴퓨터가 하는 연산의 기본은 덧셈이다. 뺄셈은 음수를 더하는 방식으로 계산한다. 다시 말해 컴퓨터가 4-2를 수행하는 과정은 4+(-2)를 연산하는 것이다. 컴퓨터에게 음수를 알려주는 방식으로는 최상위 비트(가장 왼쪽의 비트)를 이용해 최상위 비트가 0일 때는 양수, 1일 때는 음수라고 약속하면 된다. (이 방법으로 연산한 경우 overflow - 서로 부호가 다른 정수의 덧셈, 뺄셈 연산에서 발생 가능 - 가 생길 수 있다고 하는데 여기까지는 파고들지 않기로 한다...)
곱셈은 덧셈을 반복 수행하면 되고, 나눗셈은 곱셈과 달리 나머지라는 것을 처리해줘야 하고, 0으로 나눌 수 없다는 예외가 있기에 곱셉만큼 간단하지는 않다.
일단 가장 기본이 되는 덧셈을 어떻게 수행하는지가 궁금했기 때문에 이 포스팅에서는 덧셈 연산만 중점적으로 다뤄보기로 한다.
잘 알려져 있다시피 컴퓨터는 0과 1 밖에 모른다. 그렇기 때문에 0과 1을 이용해서 1비트짜리 두 수를 더하는 경우는 다음의 네 가지 밖에 없다.
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10
이 네 가지 경우를 a, b라는 입력(input)과 c(carry - 자리 올림), s(sum - 합)이라는 출력(output)으로 도식화해서 표현하면 다음과 같다.
a + b = cs
- 0 + 0 = 00
- 0 + 1 = 01
- 1 + 0 = 01
- 1 + 1 = 10
이제 이 과정을 input을 넣으면 output이 나오는 함수로 만들어 보자.
이를 구현하기 위해서는 비트 연산자 AND(&)와 XOR(^)를 사용하면 된다고 하는데.. 논리 연산자라고는 자바스크립트의 &&, ||, ! 밖에 모르기 때문에 비트 연산자의 작동 원리부터 알아보자.
AND 연산은 논리곱이라고도 하며, 곱하기처럼 작용한다. 이 연산에서는 모든 입력값이 1일 때만 1을 출력한다. (자바스크립트의 &&와 동일하다)
0 & 0 = 0
0 & 1 = 0
1 & 0 = 0
1 & 1 = 1
OR 연산은 논리합이라고도 불리며, 이는 하나 이상의 입력값이 1이면 1을 출력한다. (자바스크립트의 || 와 동일)
0 | 0 = 0
0 | 1 = 1
1 | 0 = 1
1 | 1 = 1
XOR 연산은 입력값이 같지 않으면 1을 출력한다. 다시 말해 두 비트가 서로 같으면 0을 반환하고, 서로 다르면 1을 반환한다.
0 ^ 0 = 0
0 ^ 1 = 1
1 ^ 0 = 1
1 ^ 1 = 0
참고로 NOT 연산은 비트가 0이면 1로, 1이면 0으로 반전시킨다. (자바스크립트의 !과 동일)
~0 = 1
~1 = 0
자, 그렇다면 다시 a + b = cs 를 함수로 구현하는 과정으로 돌아오자.
1) s(합)를 구하기 위해서는 어떻게 해야할까?
a, b가 서로 다를 때만 참이니 XOR 연산을 쓰면 된다.
2) c(자리올림)를 구하려면?
a, b가 같을 때만 참이니 AND 연산을 쓰면 된다.
이를 위의 진리표처럼 정리하면 다음과 같다.
c = a & b
s = a ^ b
그리고 이를 논리회로로 도식화하면 아래와 같다.
아래 D 모양의 로직 게이트는 AND, 위의 ))>는 XOR를 의미한다.
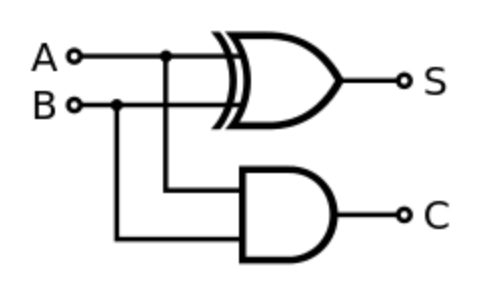

이제 우리는 1비트짜리 두 수를 더해서 최대 2비트의 출력을 가지는 덧셈기를 만들 수 있게 되었다. 이러한 덧셈 계산기를 반가산기(half adder)라고 한다. 말 그대로 반쪽짜리 계산기라는 얘기다.
왜 반쪽이라는 걸까? 그건 이전 자리 덧셈에서 올라온 자리올림 수를 고려하지 않았기 때문이다.
67 + 35 라는 덧셈을 계산하는 과정을 생각해 보자. 우리는 먼저 1의 자리에서 7과 5를 더해 12라는 숫자를 얻는다. 그리고 2는 그대로 결과의 1의 자리에 적고, 1은 10의 자리로 올려준다. 그 다음으로 10의 자리에서 6과 3을 더할 때 1의 자리수에서 자리올림으로 올라온 1을 함께 더해서 결과를 10으로 적는다. 이렇게 최종적으로 102라는 결과를 얻는다.
반가산기에서는 입력이 a, b와 두 개 뿐이었지만 실제적인 덧셈을 하려면 이전 자리의 자리올림 값도 함께 계산을 해주어야 하는 것이다. 따라서 우리는 1비트짜리 input이 세 개 들어오는 연산을 할 수 있어야 한다.
input이 A, B, Ci(C input -이전 자리올림)일 때, output으로 Co(C output - 최종자리올림), S(최종 합)를 가지는 함수를 생각해 보자.

1) 입력으로 받은 두 수 A, B를 더해 합 s1과 자리올림 c1을 구한다.
2) 합 s1과 이전 자리올림 Ci를 더해 합 s2와 자리올림 c2를 구한다.
3) 합 s2를 최종합 S로 출력한다.
4) 자리올림 c1과 자리올림 c2를 더해 최종 자리올림 Co로 출력한다.
이때, 1)과 2)의 과정은 반가산기로 더하면 된다.
4)의 과정에서 자리올림 c1과 자리올림 c2의 덧셈을 생각해 보면 c1, c2가 둘 다 1인 경우는 없기 때문에 반가산기를 쓰지 않고, OR 연산으로 대체할 수 있다.
위의 반가산기 논리회로를 아래와 같이 간략화해서 표현한다고 하면,

1) ~ 4)의 과정을 다음과 같은 논리회로로 도식화할 수 있다.
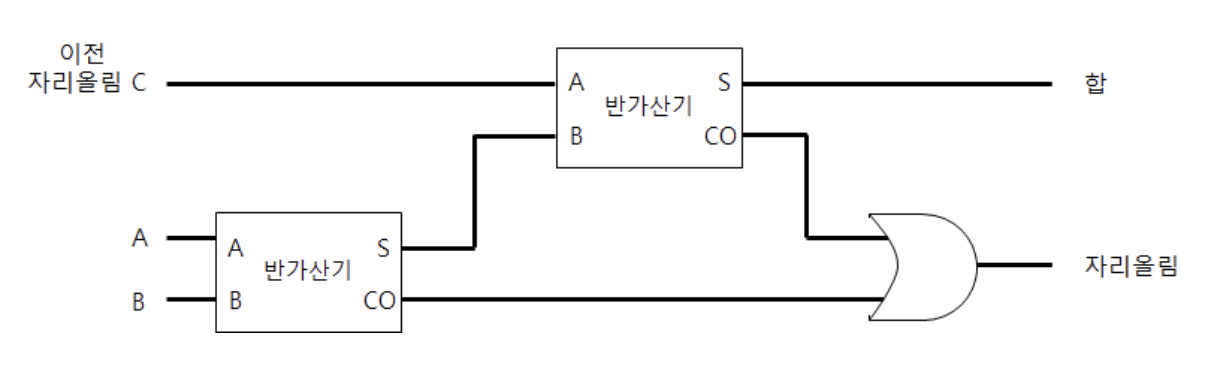
이렇게 반가산기 2개가 있어야 온전한 계산을 할 수 있기 때문에 이를 전가산기(full adder)라고 부른다.
전가산기 한 개가 한 자릿수 이진수를 더할 수 있으니 이제 두 자릿수 이진수의 덧셈을 하는 과정을 생각해 보자.
전가산기 두 개가 있으면 해결될 일인데, 두 개를 어떻게 연결해야 할까?

1) 두 자릿수 이진수 A, B의 입력을 받는다.
2) 첫번째 자리수끼리 전가산기1로 더한다.
3) 전가산기1에서 나온 자리올림 출력을 두번째 자리수의 덧셈에서 사용하는 전가산기2의 자리올림 수에 입력으로 넣는다.
4) 두번째 자리수를 자리올림 수까지 포함해 전가산기2로 더한다.
5) 결과를 출력한다.
세자리수, 네자리수도 이런 식으로 전가산기를 붙여나가면 된다. 컴퓨터의 연산 능력이 충분히 빠르기만 하다면 어떤 자릿수의 덧셈이라도 모두 구현할 수 있는 것이다.

📚 참고자료:
Khan Academy - XOR 비트 연산
https://ko.khanacademy.org/computing/computer-science/cryptography/ciphers/a/xor-bitwise-operation
[컴퓨터의 작동원리 - CODE] 6. 덧셈 계산기를 만들어 보자
https://moduweb.tistory.com/7
컴퓨터는 덧셈 만으로 사칙연산을 할 수 있다!
https://www.youtube.com/watch?v=_f5Y4fc3FX4
'배워서 남 주자' 카테고리의 다른 글
| 바닐라JS로 fetch API를 사용해 서버에 요청한 데이터 받아오는 방법 (0) | 2022.12.13 |
|---|---|
| [JavaScript] 문자열(string)을 날짜로 바꾸는 방법 (0) | 2022.12.13 |
| [React] setState는 비동기 함수일까? (0) | 2022.12.07 |
| console.log(), console.dir() 그리고 console.table() (0) | 2022.11.30 |
| 화살표 함수를 쓸 때 주의할 점 (1) | 2022.11.24 |